Em suma, a Máquina de Turing, proposta por Alan Mathison Turing (1912-1954), é um dispositivo teórico que, apesar de não ter sido implementado fisicamente na época, tornou-se a base para a computação científica. Afinal todo o processo computacional da máquina foi matematicamente demonstrado e provado no artigo intitulado “On Computable Numbers, with an Application on the Entscheidungsproblem”.

Nascido em 23 de junho de 1912 em Londres, filho de um oficial britânico, Julius Mathison e Ethel Sara Turing, Alan Mathison Turing fez-se conhecido aos 24 anos quando propôs que era possível executar operações computacionais sobre a teoria dos números por meio de uma máquina que tivesse embutidas as regras de um sistema formal.

Partindo da ideia de que um sistema formal automático é um dispositivo físico que manipula automaticamente os símbolos de um sistema formal de acordo com as regras dele, Turing propôs um dispositivo que pudesse ler e escrever símbolos em uma fita dividida em seções, definidas por ele como quadrados.
O dispositivo consistiria em uma unidade de controle que interpretaria uma lista de instruções simples sobre leitura e gravação de símbolos nos quadrados, e uma cabeça de leitura/gravação se moveria em qualquer direção ao longo da fita, um quadrado por vez, realizando as instruções, sendo que a instrução executada determina o estado da máquina.
Em resumo, a máquina de Turing move-se ou move símbolos, de uma posição para outra em uma fita de acordo com as instruções recebidas pela unidade de controle.
Porém, como a Máquina de Turing é um dispositivo hipotético, se utilizarmos seus fundamentos lógicos podemos desenvolver e implementar qualquer circuito, assim como viemos fazendo ao longo das últimas décadas.

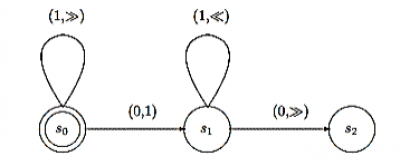
Tendo um conjunto finito de estados Q, ou seja uma lista finita de instruções, com um estado inicial distinto e um conjunto finito de símbolos Σ, neste exemplo 0 e 1, além de um branco que assume-se estar preenchendo células que não foram escritas, podemos exemplificar uma máquina de Turing com módulo de controle finito, cujas instruções estão listadas abaixo:

• imprima 0 no quadrado que passa pela cabeça
• imprima 1 no quadrado que passa pela cabeça
• vá um quadrado para a esquerda
• vá um quadrado para a direita
• vá para o passo i se o quadrado que passa pela cabeça contém 0
• vá para o passo j se o quadrado que passa pela cabeça contém 1
• pare
  

Utilizando um diagrama de estados temos que, os estados são representados por círculos, com um círculo duplo identificando o estado inicial. Uma transição de um estado para outro é representada por uma aresta ou um arco proveniente de um estado para outro ou para ele mesmo estado. As arestas são identificadas por pares (símbolo, ação), onde o símbolo é símbolo a ser lido e depois, pela ação a ser executada com a transição de um estado para outro. Os símbolos pertencem ao alfabeto Σ e a ação será o símbolo a ser escrito, ou ainda « ou », indicando um movimento para a esquerda ou direita.

A Máquina de Turing tornou-se a base fundamental para a sociedade atual, afinal através dos fundamentos lógicos dela estabelecemos o conceito de algoritmos, um dos pilares da computação e a essência por trás de qualquer computador.
Isso nos possibilitou avançar tecnologicamente e desenvolver todo o tipo de sistemas, desde a simples calculadora do seu celular até um sistema de navegação embarcado ou o piloto-automático de alguns carros e aviões, dentre muitos outros casos que beneficiaram em muito a sociedade humana.

1. “On Computable Numbers, with an Application on the Entscheidungsproblem” - A. M. TURING, disponível em: https://www.cs.virginia.edu/~robins/Turing_Paper_1936.pdf
2. Maquina de Turing - Wikipédia, a enciclopédia livre, disponivel em: https://pt.wikipedia.org/wiki/Máquina_de_Turing
3. Máquinas de Turing - Stanford Encyclopedia of Philosophy, disponível em: https://plato.stanford.edu/entries/turing-machine/
4. “A Máquina de Turing” - O. A. Pozza, S. Penedo, disponível em: https://www.inf.ufsc.br/~j.barreto/trabaluno/MaqT01.pdf
5. “Linguagens Formais” - C. A. Ferreira, disponível em: https://medium.com/@carlosalbertoff/linguagens-formais-ecf5cb08ece5