De forma abstrata, uma estrutura de dados é um formato de armazenamento de dados, com propriedades - diferentes para cada estrutura - que determinam a forma de organizar e manipular a informação utilizada pelo programa. Uma estrutura de dados é definida por uma coleção de valores, as relações entre os dados e o conjunto de operações que podem ser aplicadas em cada dado. Existem várias estruturas de dados diferentes, cada uma com suas propriedades e aplicações distintas.

Como programas de computador precisam acessar dados constantemente, estruturas de dados são fundamentais para o desenvolvimento de praticamente qualquer algoritmo e são relevantes para várias facetas da ciência da computação.

Um elemento básico de grande importância para estruturas de dados é o ponteiro, um tipo de dado que armazena um endereço de memória, usado para acessar outros valores armazenados na memória. Então, a implementação de uma estrutura de dados é, geralmente, definida pela forma com que o programa utiliza e manipula ponteiros. Um exemplo disso é o vetor, que usa um ponteiro para indicar a posição de seu primeiro elemento e então, devido a sua propriedade de armazenar dados sequencialmente, pode descobrir as posições dos elementos restantes com operações aritméticas.

Essa seção detalha brevemente propriedades de certas estruturas de dados. Note que cada linguagem de programação pode implementar essas estruturas de formas diferentes e portanto, algumas particularidades listadas aqui estarão inconsistentes com certas linguagens.

Um vetor é um conjunto de elementos armazenados sequencialmente e indexados por números inteiros. Vetores, em geral, permitem que somente um tipo de dado seja armazenado e têm tamanho fixo, definido pelo programador em tempo de compilação. Uma matriz é uma estrutura bastante similar ao vetor e pode ser entendida como um vetor de vetores.

A principal vantagem de um vetor é poder computar a posição de elementos em tempo de execução. Como os elementos de um vetor ficam lado-a-lado na memória, é possível descobrir a posição de qualquer elemento a partir do endereço do primeiro elemento e do índice atribuído. Por exemplo, considere que o primeiro elemento de um vetor indexado de 0 a 9 se encontra no endereço de memória 500 (em bytes). Supondo que esse vetor armazena variáveis com tamanho de 4 bytes, então os elementos do vetor estão ocupando os endereços 500, 504, 508, … , 536, ou seja, para um elemento de índice 5, sua posição na memória é dada por 500 + (5 * 4), ou de forma mais genérica, endereço_inicial + (índice * tamaho_do_dado). Dessa forma, um computador pode facilmente encontrar o endereço de memória de qualquer elemento de um vetor, o que torna a leitura e escrita de dados bem rápida e eficiente.

O vetor é uma das estruturas de dados mais antigas e mais usadas. Por isso, a maioria das linguagens de programação incluem uma implementação de vetores em suas bibliotecas padrão. Exemplos comuns de aplicações de vetores são:

• Renderização de imagens usando matrizes
• Implementação de tipos abstratos de dados (TAD)
• Armazenamento de strings
• Organização de dados para cálculos geométricos

A lista encadeada ou lista ligada é uma estrutura parecida com o vetor. Elementos, chamados de células, são armazenados sequencialmente, mas diferente de um vetor, eles não são indexados. Ao invés disso, células são interligadas por ponteiros.

Existem diferentes tipos de listas, classificadas pelas ligações feitas pelos ponteiros. Os tipos mais comuns são:

• Lista singularmente encadeada: cada célula contém um único ponteiro indicando a próxima célula na sequência
• Lista duplamente encadeada: cada célula contém dois ponteiros, um indicando a próxima célula da sequência e outro indicando a célula anterior da sequência
• Lista circular: tipicamente, o ponteiro de próximo elemento da última célula não aponta a nenhum objeto, mas em uma lista circular, ele aponta ao primeiro elemento da sequência

O acesso a elementos de uma lista é, em média, mais lento que acessar elementos de um vetor. Isso é porque vetores podem acessar um elemento no meio da sequência diretamente, através de aritmética simples, enquanto uma lista, para acessar uma posição n de sua sequência, precisa percorrer por todos os n - 1 elementos que o antecedem.

As principais vantagens de uma lista encadeada são relacionadas à manutenção da estrutura. Elementos podem ser inseridos e removidos sem a necessidade de trocar a posição dos outros. Além disso, o tamanho de uma lista não precisa ser definido no código fonte, o espaço de memória utilizado pode ser alocado dinamicamente (em tempo de execução), isto é, o tamanho da lista pode ser aumentado ou reduzido, conforme células são inseridas ou removidas.

Também chamado de struct (estrutura), tupla ou dado composto, o registro é um valor que armazena outros valores, tipicamente indexados por nome. Os valores armazenados são chamados de campos ou membros e geralmente podem ser de qualquer tipo, incluindo outros registros e outras estruturas de dados.

Exemplo de registros na linguagem de programação C:

struct tesouro{
   int valor;
   int peso;
   char *nome;
};

struct mochila{
   struct tesouro[200] itensGuardados;
   int capacidade;
};

Nesse exemplo, criamos um registro tesouro para representar algum objeto valioso e um registro mochila, que representa um recipiente para guardar tesouros. A partir disso, é possível criar variáveis de tipo tesouro e mochila e acessar cada campo por meio de nomeVariavel.nomeCampo. Por exemplo, considere a variável itemA de tipo tesouro e a variável mochilaA de tipo mochila. Pode-se acessar o peso de itemA através de itemA.peso e para armazenar uma cópia de itemA na mochila, é possível executar o comando mochilaA.itensGuardados[0] = itemA.

Registros são uma das estruturas de dados mais usadas para a implementação de tipos abstratos de dados, que são de grande importância para a computação.

A árvore é um tipo abstrato de dados que organiza seus elementos (chamados de nós, nodos ou vértices) baseando-se em uma hierarquia de “pais” e “filhos”. Cada nó pode ter até uma dada quantidade de filhos (especificada pelo tipo da árvore) mas necessariamente precisa ter exatamente um pai, com exceção do nó raiz, que não tem pai. De acordo com essas propriedades, pode-se afirmar que uma árvore é um tipo de grafo.

Os nós de uma árvore tipicamente armazenam uma chave e um valor. Chaves são uma forma de identificar cada elemento e são usadas para balancear a árvore de alguma forma. O valor é o objeto que deseja-se armazenar.

Exemplo de uma árvore genérica:

Algumas terminologias importantes:

• Folha (nó externo): Um nó que não tem filhos. Folhas podem ser vistas como os nós que ficam nas “pontas” da árvore
• Nó interno: Um nó que tem pelo menos um filho. Basicamente nós que não são folhas
• Subárvore: Um conjunto formado por um nó e seus descendentes. Efetivamente árvores que ficam dentro da árvore principal
• Grau: O número de filhos de um nó
• Grau da árvore: O grau máximo que um nó pode ter na árvore
• Distância: O número de vértices percorridas no menor caminho entre dois nós.
• Nível: O nível de um nó é dado pela distância entre o nó e a raiz (a raiz fica no nível 0, seus filhos no nível 1, seus netos no nível 2…)
• Altura: A distância entre um nó e a folha de maior nível. A altura da raiz é a altura da árvore

Os tipos de árvore mais comuns são:

A árvore binária de busca ou BST (do inglês, binary search tree) visa organizar seus dados de forma que os caminhos da árvore possam ser percorridos de maneira análoga à busca binária em um vetor ordenado. Em uma BST perfeitamente balanceada, uma busca por qualquer elemento é feita em ordem de complexidade O(lg n), mas no pior caso - em uma BST cuja altura é igual ao número de nós - a estrutura funciona de forma idêntica a uma lista encadeada.

Todo nó de uma BST segue as seguintes propriedades:

• seu número de filhos é no máximo dois
• sua subárvore à esquerda só contém nós com chaves menores que sua chave
• sua subárovre à direita só contém nós com chaves maiores que sua chave

No exemplo ao lado, temos uma BST não balanceada. Para melhorar seu desempenho de busca, seria necessário implementar mecanismos que reorganizem os elementos, de forma que a árvore fique balanceada.

Essa ideia foi o que motivou a criação de outros tipos de árvores, baseadas na BST, que seguem propriedades de balanceamento que garantem que a árvore, mesmo no pior caso, fique muito próxima de estar perfeitamente balanceada. Essas árvores são chamadas de auto-balanceadas, sendo as mais conhecidas a AVL e a rubro-negra.

Um exemplo real de aplicação da rubro-negra é o processo de agendamento de tarefas do Linux, chamado de CFS (do inglês completely fair scheduler).

A árvore B é uma árvore de busca auto-balanceada bastante utilizada em bancos de dados e sistemas de arquivos. Isso se dá pelo fato de que os nós de uma árvore B podem armazenar múltiplas chaves, permitindo que grandes quantidades de dados possam ser lidas de uma só vez, consequentemente minimizando o número de acessos à memória secundária. Essa propriedade permite que a quantidade máxima de filhos não seja restrita a dois, podendo generalizar para n filhos. Por isso, a árvore B pode ser vista como uma generalização de uma BST.

Um resumo das propriedades da árvore B:

• dado um valor t qualquer, o seguinte é verdade:
  • um nó deve ter no mínimo t -1 chaves
  • um nó pode ter no máximo 2t - 1 chaves
  • um nó que não seja folha deve ter no mínimo t filhos
  • um nó pode ter no máximo 2t filhos
• todas as folhas da árvore estão no mesmo nível
  • consequentemente, todos os caminhos da árvore tem a mesma altura
• as chaves de um nó estão ordenadas
• assim como na BST, valores menores são armazenados na subárvore à esquerda de uma dada chave e valores maiores são armazenados na subárvore à direita

Exemplo de uma árvore B, considerando t = 2:

A árvore trie (do inglês retrieve) ou árvore de prefixos é uma árvore de busca usada para encontrar chaves dentro de conjuntos. Diferente de outras árvores que armazenam chaves inteiras em seus nós, uma trie tipicamente armazena chaves em forma de strings, usando cada nó para representar um caractere individual. Dessa forma, entende-se que um nó qualquer na árvore representa um prefixo em comum entre todos os seu descendentes.

Como um exemplo, considere que queremos armazenar as chaves {gato, garfo, garra, ei, eita} em uma árvore trie. Uma representação visual dessa árvore seria:

Nesse exemplo, o último caractere de cada chave está marcado com um número arbitrário. Em uma implementação real, esses números poderiam representar a localização da palavra em um arquivo de texto, por exemplo. Note que ao percorrer um caminho da raiz até um nó marcado por número, uma chave completa é formada.

Árvores trie, assim como as BSTs, serviram de base para criar outros tipos de árvore mais sofisticados, como a árvore PATRICIA (ou radix), que busca diminuir o espaço de memória ocupado pela árvore.

Exemplos de aplicações reais de árvores trie:

• sistemas de correção gramatical
• busca de palavras em documentos de texto
• sugestões de completamento de palavras em editores de texto e mecanismos de busca

A tabela hash(ou tabela de dispersão) é um tipo abstrato de dados que mapeia chaves a valores em uma tabela. Ela é uma forma de implementar um vetor associativo (ou dicionário), uma estrutura que armazena seus dados de forma que não existam chaves repetidas. A principal motivação do dicionário é a otimização de operações de busca. Já que chaves não se repetem, é possível associar cada valor a uma chave única e então, o tempo de busca se torna constante, ou seja, ele não varia com a quantidade de elementos.

Um exemplo simples de implementação de dicionário é o mapeamento direto de cada chave a um índice de um vetor. Dessa forma um valor ligado a chave k é armazenado na posição k do vetor. Dessa forma, garantimos um tempo de busca constante. No entanto, essa implementação se torna extremamente ineficiente em quesitos de espaço conforme o tamaho da chave aumenta. Suponha que precisamos armazenar 2.000 itens cujas chaves usam 12 dígitos cada, variando de 000.000.000.000 a 999.999.999.999. Isso quer dizer que o vetor utilizado precisaria ter, no mínimo, 1.000.000.000.000 posições para funcionar, sendo que só 2.000 delas seriam ocupadas.

Uma solução para esse problema é, justamente, a tabela hash. A ideia básica por trás dela é utilizar uma função hash (ou função de espalhamento) para calcular um local de armazenamento para cada chave. Em um cenário ideal, essa função é capaz de produzir um índice único para cada chave. mas nem sempre isso é possível. Existem situações em que múltiplas chaves geram posições idênticas - isso é chamado de colisão - e o programa precisa implementar alguma estratégia para resolver esse conflito. A eficiência de uma tabela hash depende fortemente de uma função que minimize o número de colisões.

Para ilustrar um exemplo, considere que temos um jogo que identifica as contas dos jogadores por um ID de usuário. Os IDs servirão de chaves para montar uma tabela hash armazenando informações de cada conta, como nome de usuário. A primeira coluna armazena a chave associada àquela posição, a segunda coluna armazena o valor associado:

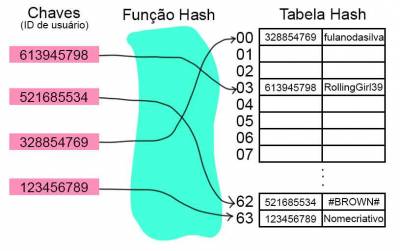
Algumas aplicações comuns da tabela hash:

• bancos de dados
• caches
• armazenar qualquer conjunto de dados sem elementos repetidos

1. WEGNER, Peter; REILLY, Edwin D. Data Structures. ACM Digital Library. Disponível em: https://dl.acm.org/doi/10.5555/1074100.1074312. Acesso em: 25 agosto. 2022.
2. Estruturas de dados. Wikipedia. Disponível em: https://pt.wikipedia.org/wiki/Estrutura_de_dados. Acesso em: 25 agosto. 2022.
3. Array data structure. Wikipedia. Disponível em: https://en.wikipedia.org/wiki/Array_data_structure. Acesso em: 27 agosto. 2022.
4. FEOFILOFF, Paulo. Listas encadeadas. IME-USP. Disponível em: https://www.ime.usp.br/~pf/algoritmos/aulas/lista.html. Acesso em: 28 agosto. 2022.
5. Record (computer science). Wikipedia. Disponível em: https://en.wikipedia.org/wiki/Record_(computer_science). Acesso em: 27 agosto. 2022.
6. FEOFILOFF, Paulo. Árvores binárias de busca. IME-USP. Disponível em: https://www.ime.usp.br/~pf/algoritmos/aulas/binst.html. Acesso em: 28 agosto. 2022.
7. CFS Scheduler. The Linux Kernel documentation. Disponível em: https://www.kernel.org/doc/html/latest/scheduler/sched-design-CFS.html. Acesso em: 28 agosto. 2022.
8. SCHREINER, Marcos Antonio. Árvores B. UFPR. Disponível em: https://docs.ufpr.br/~marcosantonio/disciplinas/algIII/arvoreB.pdf. Acesso em: 28 agosto. 2022.
9. Trie. Wikipedia. Disponível em: https://en.wikipedia.org/wiki/Trie. Acesso em: 28 agosto. 2022.
10. Introduction to hashing. GeeksforGeeks. Disponível em: https://www.geeksforgeeks.org/hashing-set-1-introduction/. Acesso em: 29 agosto. 2022.
11. Associative array. Wikipedia. Disponível em: https://en.wikipedia.org/wiki/Associative_array. Acesso em: 29 agosto. 2022.